R1 Regularization

Which Training Methods for GANs do actually Converge?

Table of contents

  1. Introduction
  2. Instabilities in GAN training
    1. Dirac-GAN
    2. Where do instabilities come from?
  3. Regularization strategies
    1. Wasserstein GAN
    2. Instance noise
    3. Zero-centered gradient penalties
  4. General convergence results
    1. Simplified gradient penalties
    2. Convergence
    3. Stable equilibria for unregularized GAN training
  5. Experiments

최근 연구에서 GAN training이 특정 조건 하에서 local convergence하다는 것을 보였음
즉, 실제 data distribution과 generated data distribution이 absolute continuity일 때, gan 훈련이 안정적으로 진행됨

Absolute Continuity

한 measure(측도)가 다른 측도에 완전히 “연속적”으로 의존하는 관계를 의미
즉, 두 measure \(\mu, v\)가 있을 때, 다음을 만족하면 \(\mu\)가 $v$$에 대해 absolute continuous

\[\text{If }v(A)=0\text{, then } \mu(A)=0 \text{ for all measurable sets A.}\]

Measure는 집합에 대해 ‘크기’나 ‘양’을 할당하는 함수로, 이것을 통해 확률 공간(probability space) 내의 사건들에 확률을 할당할 수 있음 (확률 측도)
\(\rightarrow\) 일반적인 사진 데이터셋에서 풍경 사진에 대한 측도가 높다는 것은 해당 data 집합에 풍경 사진이 많이 포함되어 있다는 것을 의미함

두 확률 분포 사이의 측도는 KL Divergence, Jensen-Shannon Divergence, Wasserstein Distance 등으로 계산할 수 있음

GAN에서 Absolute Continuity하다는 것은 generated data가 dataset의 분포를 잘 따라갔다는 것을 의미 즉, 저자는 Absolute Continuity일 때, GAN의 훈련이 안정적으로 진행되는 이전 연구들을 언급하며 Absolute Continuity는 필수적이고, 일반적인 상황에서 GAN 훈련이 안정적으로 진행될 수 있는 regularizer를 제시할 예정

논문에서는 absolute continuity가 필수적이라는 것을 보이며 안정적인 GAN 훈련에 대한 regularization strategy를 discuss
\(\rightarrow\) instance noise, zero-centered gradient penalty 들은 수렴했지만, Wasserstein-GAN, WGAN-GP는 수렴하지 않을 때도 있었음

추가적으로 일반적인 GAN에 대해 regularizer를 확장하고 단순화된 gradient panelty 방식을 제안함

Introduction

최근 연구에서, gradient vector field의 Jacobian의 eigenvalue를 통해 GAN training의 property를 분석할 수 있다는 것을 보임
Jacobian이 equilibrium point에서

  • 음의 실수부를 갖는 eigenvalue만 갖는 경우 GAN training은 local convergence
  • 허수축을 가지면 일반적으로 local convergence가 아님
  • 허수축이 없지만, 가까운 경우, 작은 lr이 요구됨
    \(\rightarrow\) Unstability의 원인이 이것인지는 규명되지 않음

논문에서 contribution은

  1. 정규화되지 않은 GAN training이 항상 수렴되지는 않음을 원형적인 반례를 통해 보임
  2. 최근 제안된 regularization technique들에 대한 stabilize 여부 논의
  3. 단순화된 gradient panelty를 제안하고 local convergence를 증명

Instabilities in GAN training

GAN은 generator, discriminator의 parameter가 각각 \(\theta, \phi\)로 정의될 때, Nash-equilibrium \((\theta^*, \phi^*)\)을 찾는 것을 목표로 함

Gradient Vector Field (GVF)를

\[\begin{align} v(\theta, \phi) = \begin{pmatrix} -\nabla_\theta L(\theta, \phi) \\ \nabla_\phi L(\theta, \phi)\end{pmatrix} \end{align}\]

라고 할 때, SimGD (simultaneous gradient descent)는

\[F_h(\theta, \phi) = (\theta, \phi) + hv(\theta, \phi)\]

로 표현할 수 있음
The Numerics of GANs에서는 이를 바탕으로 equilibrium point로의 수렴을 조사

The Numerics of GANs Simultaneous Gradient Ascent (SimGA)에서 두 network가 서로의 변화에 적응적으로 equilibrium point를 찾아야하기 때문에 훈련이 안정적이지 않다는 문제가 있음
또한, GVF의 Jacobian의 eigenvalue 실수부가 0에 가까우면서 허수부가 클 때, 수렴이 느리거나 발산하는 경우가 있음을 확인함
(실수부가 모두 0이면 sublinear하게 수렴) 이에, GVF를 $$ \begin{align} w(x)=v(x)-\gamma\nabla L(x), \quad \nabla L(x) = v'(x)^T v(x) \end{align} $$ 로 변경하여 regularization term을 적용함
위의 방식이 local convergence하다는 것을 보임으로써 안정적인 GAN training을 제안

Equilibrium point 근처에서 GAN training의 local convergence를 Jacobian \(F'_h(\theta, \phi)\)의 spectrum을 통해 분석할 수 있음

  • \(F'_h(\theta, \phi)\)가 절대값이 1보다 큰 eigenvalue를 가지고 있으면, training algorithm은 equilibrium point \((\theta^*, \phi^*)\)로 수렴하지 않음
  • Eigenvalue가 1보다 작으면, \(\mathcal{O}(\vert\lambda_{max}\vert^k)\)의 linear rate로 equilibrium point \((\theta^*, \phi^*)\)에 수렴함
  • 실수부가 모두 0이면 sublinear하게 수렴

Learning rate가 극단적으로 작은 continuous system

\[\begin{align} \begin{pmatrix} \dot{\theta}(t) \\ \dot{\phi}(t) \end{pmatrix} = \begin{pmatrix} -\nabla_\theta L(\theta, \phi) \\ \nabla_\phi L(\theta, \phi) \end{pmatrix} \end{align}\]

에서도 비슷하게 적용됨

  • Jacobian \(v'(\theta^*, \phi^*)\)의 stationary point \((\theta^*, \phi^*)\)에서 모든 eigenvalue가 negative real-part를 가지고 있으면 linear convergence rate로 수렴
  • \(v'(\theta^*, \phi^*)\)의 eigenvalue가 positive real-part를 가지고 있으면 locally 수렴하지 않음

Dirac-GAN

Unregularized GAN은 locally, globally convergence하지 않다는 것을 간단한 반례로 보임

Definition 2.1 Dirac-GAN은 실험을 위해 \(p_\theta = \delta_\theta, D_\phi(x)=\phi\dot x\)로 구성됨
실제 데이터 분포 \(p_{\mathcal{D}}\)는 0 중심의 Dirac-distribution으로 나타남

\[\begin{align} L(\theta, \phi)=f(\phi, \theta) + f(0) \end{align}\]
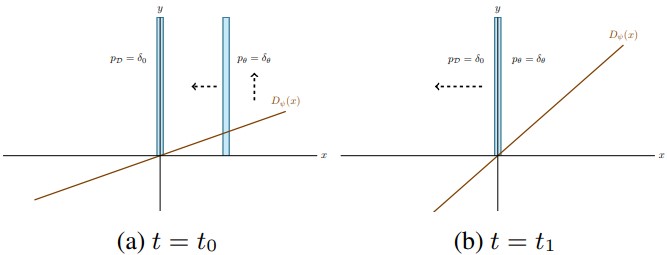
Figure 1
[Figure 1]

초기에는 \(p_{\mathcal{D}}\)의 방향으로 훈련되게 되지만, distribution이 real에 가까워질수록 \(\phi\)의 절댓값이 커지기 때문에 0 근처에서 distribution이 진동을 하게됨
\(\rightarrow\) Convergence하지 않음

Lemma 2.2 식 (4)의 unique Ep(equilibrium point)는 \(\theta=\phi=0\). Ep에서 GVF의 Jacobian은 \(\pm f'(0)i\)의 2개의 허수축을 가짐 \(\rightarrow\) Numerics of GANs에 따르면, sublinear하게 수렴된다고 볼 수 있지만, 다음 Lemma에서 사실이 아님을 밝힘

Lemma 2.3 GFV \(v(\theta, \phi)\)의 integral curve는 Nash-equilibrium으로 convergence하지 않음

Where do instabilities come from?

Regularization strategies

Wasserstein GAN

Instance noise

Zero-centered gradient penalties

General convergence results

Simplified gradient penalties

Convergence

Stable equilibria for unregularized GAN training

Experiments