Fast Sampling of Diffusion Models with Exponential Integrator

Fast Sampling of Diffusion Models with Exponential Integrator
ODE를 이산화하고, error를 줄이기 위해 semilinear structure 이용

Table of Contents

  1. Introduction
  2. Background
  3. Fast Sampling with Learned Score Models
    1. Can We Learn Globally Accurate Score?
    2. Discretization Error
      1. Probability Flow ODE (\(\lambda=0\))
      2. Ingredient 1.
      3. Ingredient 2.
      4. Ingredient 3.

Introduction

Diffusion model은 기본적으로 diffusion process와 reverse process로 이뤄짐
\(\rightarrow\) Time-dependency score function을 배우기 때문에 score-based model이라고 불림
\(\rightarrow\) 다른 model보다 scalability가 좋고, hyperparam에 덜 민감
\(\rightarrow\) 대부분의 task에서 좋은 performance를 보임

하지만 recurrence process로 인해 inference time이 느리기 때문에 이를 빠르게 하기 위한 방법들이 연구됨

\(\rightarrow\) 효율적인 reverse를 위한 forward 수정 및 변경 (DDIM)
\(\rightarrow\) Numerical Solber or SDE (Score-SDE, DPM, etc…)
\(\rightarrow\) 위 두 방법을 모두 적용: PNDM

DDIM은 Scored-SDE의 Probabilistic Flow ODE의 이산화와 같다고 볼 수 있지만, Euler와 같은 일반적인 이산화가 왜 잘 동작하는지 밝혀지지 않음
따라서, 빠른 sampling을 위해 DM reverse의 일반화된 이산화 방법을 설립함
\(\rightarrow\) DM과 관련된 ODE/SDE, fitting error, discretize error에 대해서 조사

같은 DM이어도 이산화 방법에 따라 error가 크게 달라짐
따라서, DEIS는
\(\rightarrow\) Semilinear structure를 이용한 Exponential Integral(EI)가 가장 작은 error를 가진다는 것을 보임
\(\rightarrow\) Discretize Error를 더 줄이기 위해 ODE의 비선형을 근사하기 위한 다항식이나 변형된 ODE에 Runge-Kutta를 적용

Contribution:

  1. 빠른 sampling을 위한 marginal ODEs/SDEs 계열에 대한 조사 및 이에 대한 numerical solver error 조사
  2. DM에 일반적으로 적용할 수 있는 제한된 NFE에서 뛰어난 sampling quality를 보이는 DEIS 제안
  3. DDIM의 discretization을 정당화하고, DDIM이 DEIS의 한 종류라는 것을 증명
  4. DEIS 성능 실험

Background

  • Forward NOise Diffuion
\[\begin{align} \text{SDE: } dx=\mathbf{F}_txdt+\mathbf{G}_tdw, \end{align}\]
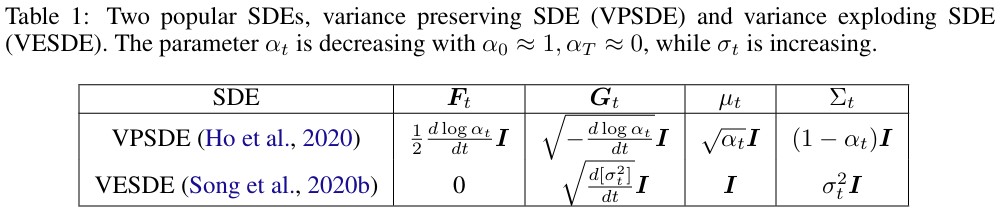
Figure 1
  • Backward Denoising Diffusion
\[\begin{align} x=\left[ \mathbf{F}_txdt-\mathbf{G}_t\mathbf{G}_t^T\nabla\log p_t(x)\right]dt + \mathbf{G}_tdw, \end{align}\]
  • Training
\[\begin{align} L(\theta)=\mathbb{E}_{t\sim \text{Unif}[0, T]}\mathbb{E}_{p(x_0)p_{0t}(x_t\mid x_0)}\left[ \parallel \nabla\log p_{0t}(x_t\mid x_0)-s_\theta(x_t,t) \parallel^2_{\Lambda_t} \right] \end{align}\]

Fast Sampling with Learned Score Models

\(s_\theta(x, t)\simeq\nabla\log p_t(x)\)가 학습되면 backward SDE를 통해 sampling 할 수 있고
\(\lambda \ge 0\)일 때, SDE 군을 고려하면 (일반화)

\[\begin{align} d\hat{x}=\left[\mathbf{F}_t\hat{x}-\frac{1+\lambda^2}{2}\mathbf{G}_t\mathbf{G}_t^Ts_\theta(\hat{x},t) \right]dt+\lambda\mathbf{G}_tdw \end{align}\]

\(\rightarrow\) \(\lambda=0\)이면 Scored-SDE의 probability flow ODE \(\rightarrow\) \(\lambda=1\)이면, eq.2

Proposition 1.
When \(s_\theta(x,t)=\nabla\log p_t(x)\) for all \(x,t\), and \(\hat{p}^*_T=\pi\), the marginal distribution \(\hat{p}^*_t\) of Eq.(4) matches \(p_t\) of the forward diffusion Eq.(1) for all \(0<t\leq T\)

  • Fitting Error: \(s_\theta\)와 \(\nabla\log p_t(x)\)의 차이
  • Discretization Error: Eq.4의 Discretization Error DEIS는 \(\lambda=0\)을 중심으로 위 두 error를 줄이기(해결하기) 위한 연구이고, VPSDE를 기준으로 함

Can We Learn Globally Accurate Score?

Diffusion의 성공으로 인해, fitting error가 작다고 생각되지만, 실제로는 큼

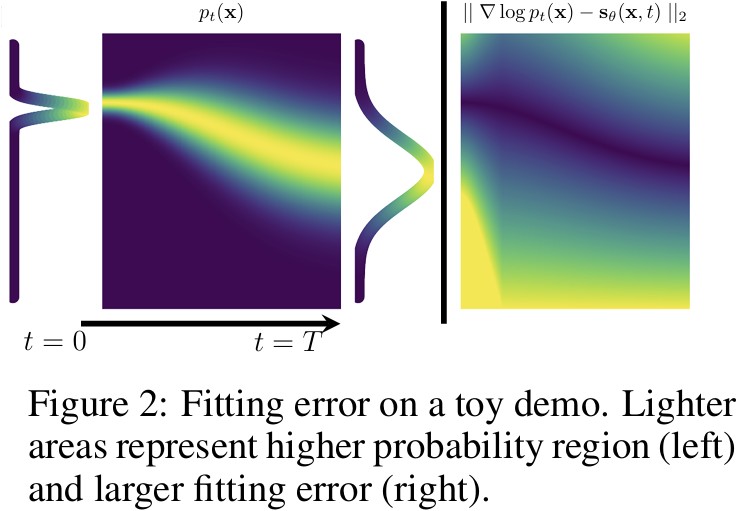
Figure 2

\(\rightarrow\) \(p_t(x)\)의 region이 작으면 error \(\uparrow\), 크면 error \(\downarrow\)
즉, 낮은 \(p_t(x)\) 값(낮은 확률)에서는 훈련된 score가 부정확함 (이미지같은 고차원 data는 작은 manifold에 모여있음)

\(\hat{x}_t\)의 품질을 높이려면 모든 \(t\)에서 \(p_t(x)\)가 높아야 함
\(\rightarrow\) 큰 step을 취하는 것이 힘듦
\(\rightarrow\) 좋은 이산화는 fitting error를 줄일 수 있어야 함

Discretization Error

Probability Flow ODE (\(\lambda=0\))
\[\begin{align} \frac{d\hat{x}}{dt}=\mathbf{F}_t\hat{x}-\frac{1}{2}\mathbf{G}_t\mathbf{G}_t^Ts_\theta(\hat{x},t) \end{align}\]

이에 대한 정확한 solution은 아래 조건을 만족할 때, 다음과 같이 나타남

  1. \(\psi(t,s)\)는 \(\frac{\partial}{\partial t}\psi(t,s)=\mathbf{F}_t\psi(t,s)\)
  2. \(\psi(t,s)=I\)가 time \(s\mapsto t\)까지의 transition matrix
\[\begin{align} \hat{x}_t=\Psi(t,s)\hat{x}_s+\int^t_s\Psi(t,\gamma)\left[-\frac{1}{2}\mathbf{G}_\gamma\mathbf{G}_\gamma^Ts_\theta(\hat{x}_\gamma,\gamma) \right]d\gamma \end{align}\]

Eq.5가 linear term \(\mathbf{F}_t\hat{x}\)와 nonlinear term \(s_\theta(\hat{x},t)\)로 구성된 semilinear stiff ODE
Eq.6를 근사하기 위해 다양한 이산화 scheme과 관련된 eq.5에 대한 다양한 numerical solver가 있음
이산화 step size가 0으로 가면, 모든 solution이 eq.5로 수렴

뒤의 Ingredient에서 큰 step size를 위해 eq.5의 discretization error를 조사하고,
작은 수의 NFE(Neural Function Evaluation)가 요구되는 algorithm 제안

Ingredient 1.

Ingredient 2.

Ingredient 3.