Adaptively-Realistic Image Generation from Stroke and Sketch with Diffusion Model

Adaptively-Realistic Image Generation from Stroke and Sketch with Diffusion Model

Table of Contents

  1. Introduction
  2. Method
    1. Preliminaries
    2. Sketch- and Stroke-Guided Diffusion Model
    3. Realism Control
  3. Experiments
    1. Qualitative Evaluation
    2. Quantitative Evaluation
  4. Conclusion

DM을 기반으로 sketch와 stroke의 이미지 합성에 대한 3차원 control이 가능한 framework 제안
User input과 faithfulness level 조절 가능

Introduction

스케치와 획은 사물과 장면을 추상적으로 묘사한 것
GAN은 stroke, sketch에 대해 따로 모델이 필요하고 control과 flexible이 부족

따라서, input의 consistency에 대한 3차원(contour, color, realism) control이 가능하고 sketch, stroke에서 이미지를 생성하는 DM framework DiSS 제안

Method

Sketch와 stroke를 condition으로 하여, realism과 condition에 대한 faithfulness를 3차원으로 조절할 수 있는 이미지 생성을 목표로 함

Preliminaries

DDPM은 simple distribution에서 target distribution까지 mapping하기 위해 diffusion process를 적용한 생성 모델의 한 종류

Forward는 target distribution으로부터 add noise

\[\begin{align} q(x_t|x_{t-1})&=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_tI), \\ q(x_t|x_0)&=\mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)\epsilon),\\ x_t&=\sqrt{\bar{\alpha}_t}x_0+\sqrt{(1-\bar{\alpha}_t)\epsilon} \end{align}\]

Backward는 reverse 과정을 학습

\[\begin{align} p_\theta(x_{t-1}|x_t)&=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\sum_\theta{(x_t,t)}),\\ \mu_\theta(x_t,t)&=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t,t)) \end{align}\]

위 두 과정 모두 Markov chain

\[L_{\mathrm{simple}}=E_{t\sim[1,T],x_0\sim q(x_0),\epsilon\sim\mathcal{N}(0,I)}[\lVert\epsilon-\epsilon_\theta(x_t,t)\rVert^2],\]

Improved DDPM에선 fixed covariance의 upper, lower bound를 interpolate하기 위해 \(L_{vlb}\) 추가

Sketch- and Stroke-Guided Diffusion Model

주어진 sketch와 stroke에 대해 이미지를 생성하기 위해, input \(x_t\)와 concate 하여 U-Net model에 input으로 사용됨

따라서, condition에 대해 parameterize된 gaussian transition은

\[\hat{p}_\theta(\tilde{x}_{t-1}|x_t,\mathrm{c}_\mathrm{sketch},\mathrm{c}_\mathrm{stroke})=\mathcal{N}(\tilde{x}_{t-1};\mu_\theta(x_t,t,\mathrm{c}_\mathrm{sketch},\mathrm{c}_\mathrm{stroke}),\sum_{\theta}(x_t,t,\mathrm{c}_\mathrm{sketch},\mathrm{c}_\mathrm{stroke}))\] \[\hat{L}_\mathrm{simple}=E_{t,x_0,\epsilon}[\lVert\epsilon-\hat{\epsilon}_\theta(x_t,t,\mathrm{c}_\mathrm{sketch},\mathrm{c}_\mathrm{stroke})\rVert^2]\]

Stroke와 sketch의 guidance level을 조절하기 위해, Classifier-free guidance를 사용

\(\rightarrow\) condition이 있는 것과 없는 것을 모두 훈련시키는 것

본 task에 적용하기 위해, two-dimensional guidance로 변경

\(\rightarrow\) Two-stage training을 사용함

  1. Sketch와 stoke를 모두 condition으로 사용하여 훈련
  2. 각 condition을 30%의 확률로, gray pixel로 채워진 이미지 \(\Phi\)로 대체
    1. Sampling 도중에, condition의 신뢰도는 두 guidance scale \(s_\mathrm{sketch}, s_\mathrm{stroke}\)의 linear combination으로 조절됨
\[\begin{align} \hat{\epsilon}_\theta(x_t,t,\mathrm{c}_\mathrm{sketch},\mathrm{c}_\mathrm{stroke})&=\hat{\epsilon}_\theta(x_t,t,\Phi,\Phi)\\ &+s_\mathrm{sketch}(\hat{\epsilon}_\theta(x_t,t,\mathrm{c}_\mathrm{sketch},\Phi)-\hat{\epsilon}_\theta(x_t,t,\Phi,\Phi))\\ &+s_\mathrm{stroke}(\hat{\epsilon}_\theta(x_t,t,\Phi,\mathrm{c}_\mathrm{stroke})-\hat{\epsilon}_\theta(x_t,t,\Phi,\Phi)) \end{align}\]

이를 통해, diffision model에서 multi-guidance를 제공

Realism Control

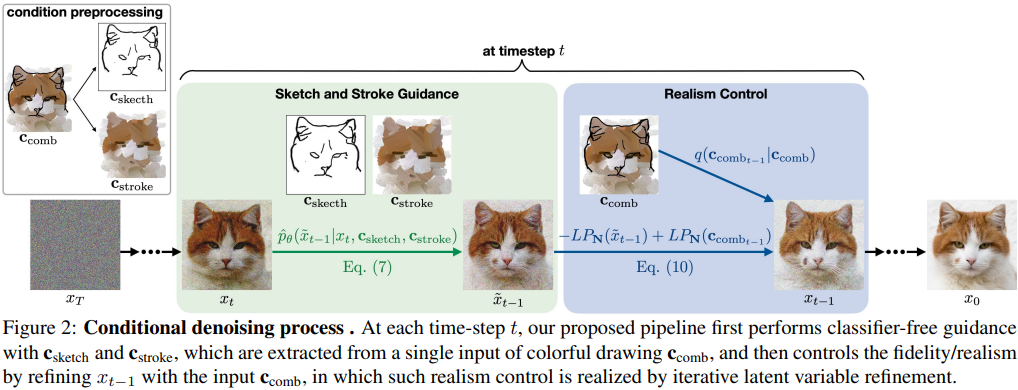
Figure 1
[Figure 1]

입력이 항상 realistic하지 않기 때문에 입력에 얼마나 faithful 할 지에 대한 control이 필요
\(\rightarrow\) output이 얼마나 realistic할지
\(\rightarrow\) two-dimensional classifier-free guidance
\(\rightarrow\) reference image는 downsample되어, condition으로 넣어짐
\(\rightarrow\) Target distribution인 real image와 condition 간의 trade-off

\(LP\)를 linear low pass filtering이고, \(N\)이 down 후 up 의 size라고 할 때,

Realism weight \(s\sim[0, 1]\) (Transformed size \(N\)을 의미)와 sketch, stroke 결합인 \(c_\mathrm{comb}\)가 \(m*m\)크기로 주어지면, conditioning generative process는

\[\begin{align} \tilde{x}_{t-1}&\sim\hat{p}_\theta(\tilde{x}_{t-1}|x_t,\mathrm{c}_\mathrm{sketch},\mathrm{c}_\mathrm{stroke}),\\ x_{t-1}&=\tilde{x}_{t-1}-LP_N(\tilde{x}_{t-1})+LP_N(c_{\mathrm{comb}{t-1}}),\\ &\mathrm{where}\;\;N=-s_{\mathrm{realism}}(\frac{m}{8}-1)+\frac{m}{8}+k \end{align}\]

\(c_\mathrm{comb}\)도 \(x_t\)마찬가지로, \(c_\mathrm{comb0}\)에서 noise를 넣은 것임
즉, 수식은 \(x_{t-1}\)에서 high-freq를 살리고, condition에서 low-freq를 가져온 것

이후 연구들

ILVR은 lowpass-filter를 교체하는 방식으로 동작하는데, 이것이 noise의 manifold에 맞지 않다는 후속 연구가 있음
\(\rightarrow\) (MCG) Improving Diffusion Models for Inverse Problems using Manifold Constraints
\(\rightarrow\) draft process의 trajectory가 있을 때, lowpass-filter는 단순하 trajectory에 projection하는 것과 같다고 함
따라서, diffusion의 단계가 어긋나는 것과 같다고 생각할 수 있음

해당 step의 manifold에 맞게 reference를 주는 방법을 MCG 제안함
\(\rightarrow\) 제대로 읽지 않아서 다시 읽어봐야 함

이런 방식으로 DiSS의 성능과 boundary artifact를 확인해볼 수 있을 듯

Experiments

Generative Process에서 contour, color, realism에 대한 control과 application(multi conditioned local editing, region-sensitive stroke-to-image (부분만 color를 줌)), control의 trade-off에 대해서 조사

Datasets.
AFHQ, Landscapes, Oxford Flower 사용

사진으로부터 sketch 얻기(condition): Photo-sketching

사진으로부터 stroke 얻기(condition): Stylized neural painting, paint transformer

Compared methods.

Qualitative Evaluation

Adaptively-realistic image generation from sketch and stroke.

Figure 2
[Figure 2]

Multi-modal multi-domain translation.
확률 모델이기 때문에 여러 이미지를 생성할 수 있음
Sketch는 어느 정도 class의 정보를 포함함을 알 수 있음
또한 sketch와 stroke가 다른 이미지에서 와도 생성이 잘됨 (un-aligned에 robust)

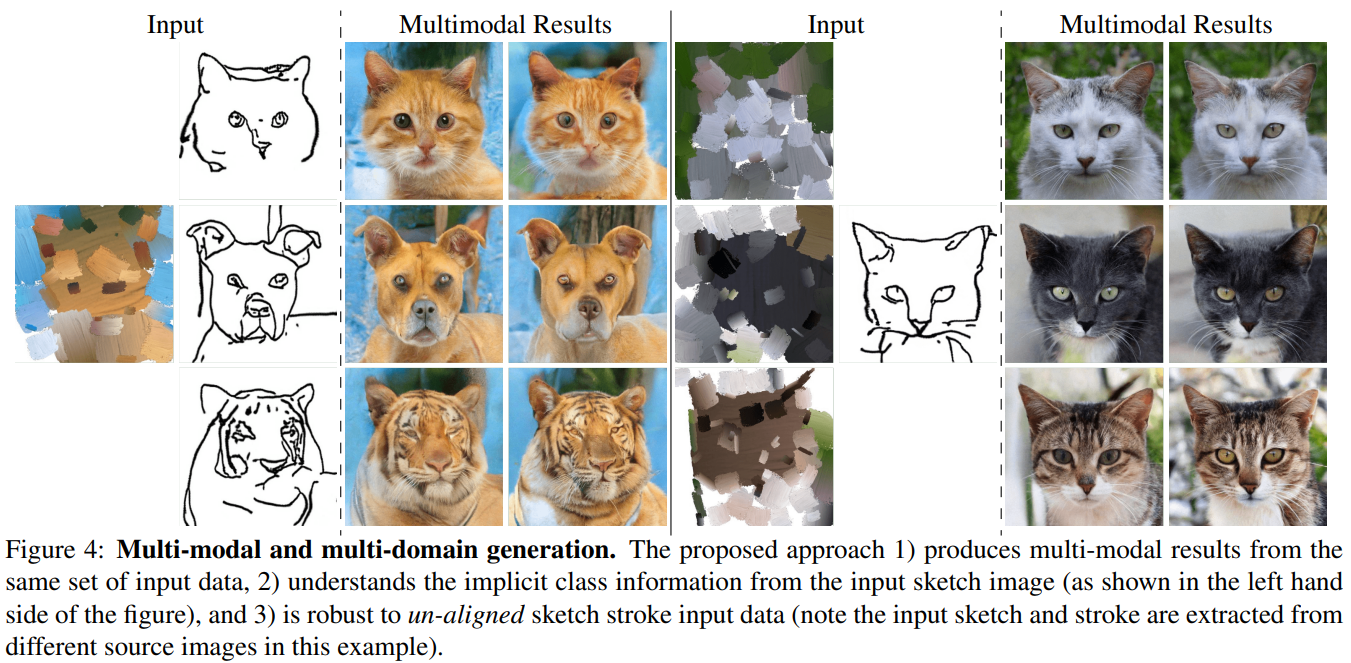
Figure 3
[Figure 3]

Applications.

3차원 control에 더불어, local 영역 편집 및 영역 stroke-to-image도 가능

  • Inference algorithm만 변경하면 application 가능
Figure 12
[Figure 12]
Figure 4
[Figure 4]
Figure 5
[Figure 5]
Figure 6
[Figure 6]

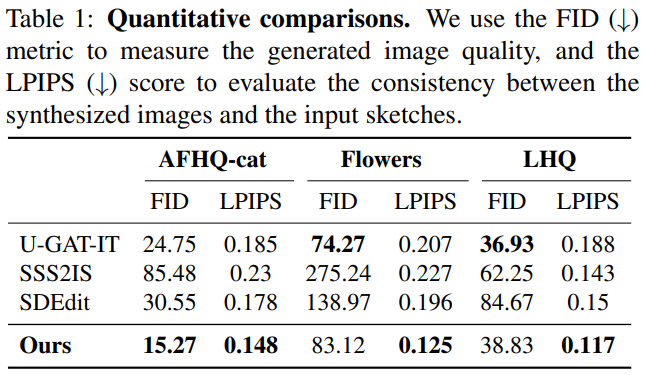
Quantitative Evaluation

Image quality and correspondence to input sketch.

Figure 7
[Figure 7]

Realism vs correspondence to input guidance.

Figure 8
[Figure 8]

Controlling stroke and sketch scales.

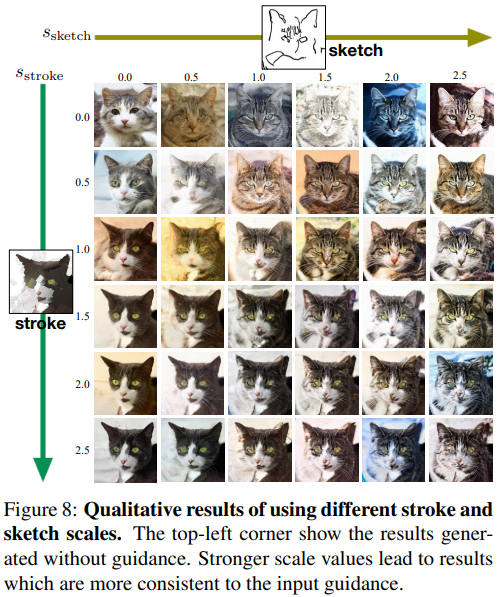Figure 9
[Figure 9]
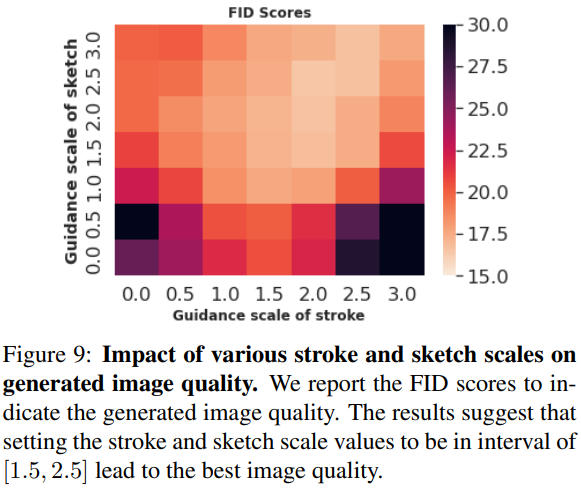Figure 10
[Figure 10]

Conclusion

Sketch과 colored stroke를 통해 flexible하게 photo-realistic images를 생성하는 DiSS framework 제안

  1. Two-directional classifier-free guidance
  2. Iterative latent variable refinement
Figure 11
[Figure 11]