On the Importance of Noise Scheduling for Diffusion Models
On the Importance of Noise Scheduling for Diffusion Models
Table of contents
- Why is noise scheduling important for diffusion models?
- Strategies to adjust noise scheduling
- Experiments
- Reference
노이즈 스케줄링 전략의 효과를 경험적으로 기록한 tech reports
- 노이즈 스케줄링은 성능에 중요하며 최적의 스케줄링은 작업(예: 이미지 크기)에 따라 다름
- 이미지 크기를 늘리면 최적의 노이즈 스케줄링이 더 노이즈가 많은 쪽으로 이동(픽셀의 중복성 증가로 인해)
- 노이즈 일정 함수를 고정한 상태로 유지하면서 단순히 입력 데이터를 b의 계수로 스케일링하는 것은 이미지 크기 전반에 걸쳐 좋은 전략
Why is noise scheduling important for diffusion models?
DDPM과 같은 diffusion modele들은 \(x_t =\sqrt{\gamma(t)}x_0+\sqrt{1-\gamma(t)}\epsilon\)로 forward를 정의
Reverse에서 \(\epsilon\)이나 \(x_0\)를 예측하도록 훈련함
Noise level \(\gamma(t)\)은 훈련되는 잡음의 분포를 결정함
Noise scheduling은 네트워크에서 중요한 역할을 함
이미지의 크기가 커지면, noise를 제거하기 쉬워짐
\(\rightarrow\) 자연적인 이미지는 local에서 중복성을 나타내기 때문에 독립적인 noise가 적용되면 정보의 파괴가 적어짐 (noise2noise에서 활용한 개념이랑 다르지만 비슷한 듯)
\(\rightarrow\) 이어서, 이미지의 크기가 커지면, denoising을 더 쉽게 할 수 있음
따라서, 작은 resolution에서와 높은 해상도에서의 optimal scheduling은 다를 수 있음

Strategies to adjust noise scheduling
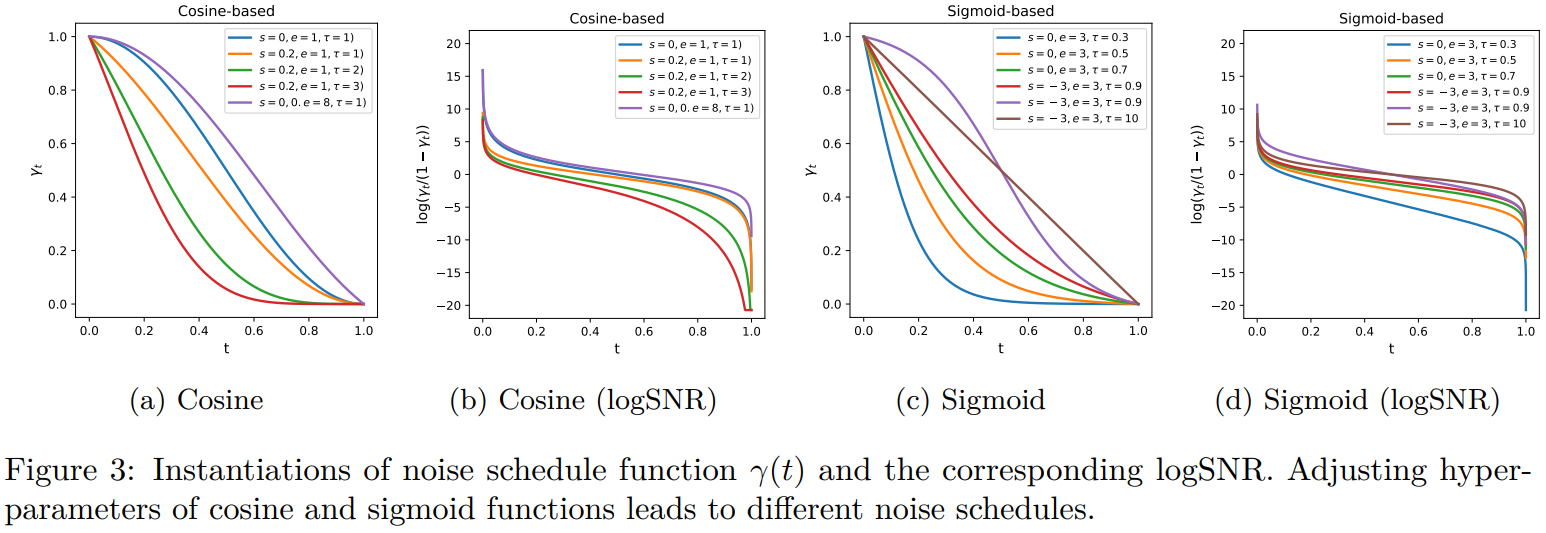
Strategy 1: changing noise schedule functions
1차원 함수로 noise schedule을 변수화하는 방법 (ex. cosine, sigmoid, linear functions)
Strategy 2: adjusting input scaling factor
간접적으로 noise의 scale을 조정하는 방법은 A Generalist Framework for Panoptic Segmentation of Images and Videos에서와 같이 \(x_0\)을 상수 b로 scaling하는 것
\[x_t =\sqrt{\gamma(t)}bx_0+\sqrt{1-\gamma(t)}\epsilon\]b가 줄어들면 noise level이 올라감

하지만, b는 variance에 영향을 줄 수 있고, 이는 성능 저하를 야기할 수 있음
따라서, variance를 고정시키기 위해 \(\frac{1}{(b^2 - 1)(\gamma(t)+1)}\)같이 scale을 할 수 있음
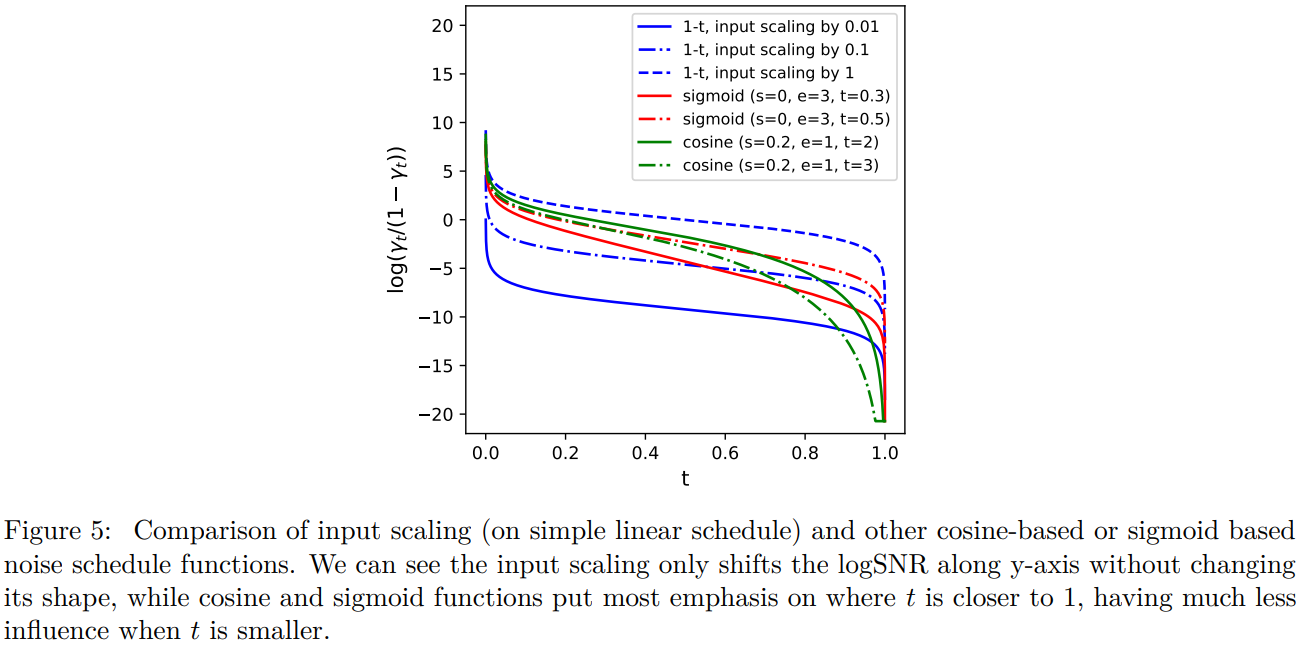
더 간단하게, denoising network에 입력 전에 scaling하는 것도 잘 동작함
아래의 그림과 같이, scheduling 모양이 변하지 않고 scale만 변하는 것을 확인할 수 있음
Putting it together: a simple compound noise scheduling strategy
저자는 \(\gamma(t)=1-t\)와 같은 간단한 scheduling과 입력의 scaling을 이용한 noise scheduling 제안

sampling 시에도 normalization을 해주어야함
continuous 하게 학습이 되어서, 이산화는 마음대로 해도 되지만, cosine이 효율적임

Experiments
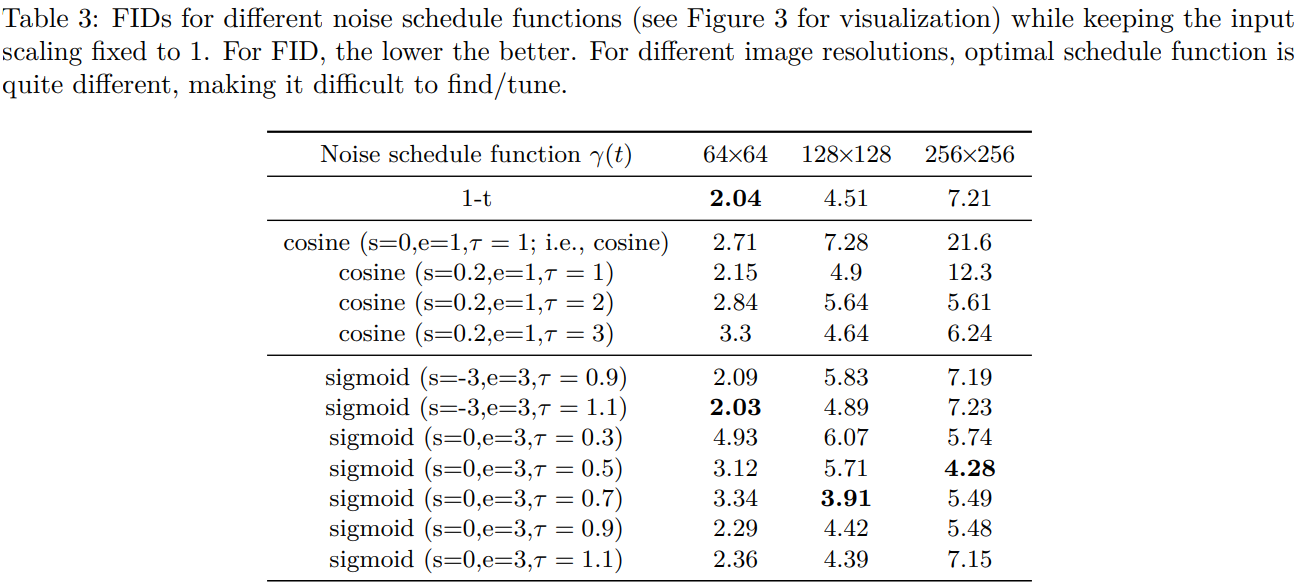
The effect of strategy 1 (noise schedule functions)
input scale을 조정하지 않고, image resolution에 따른 optimal scheduling을 조사해봄 (cosine, sigmoid scheduling에 대해)
image resolution마다 optimal schedule이 달랐음
\(\rightarrow\) 대체적으로 resolution이 커지면, 큰 T에서 느린 schedule이 효과를 갖는 듯
\(\rightarrow\) 이미지의 크기가 커지면 인근 픽셀간의 복제가 커지기 때문에, 낮은 t에서는 noise의 영향이 작아짐
개인적으로, 중심극한정리 때문도 있을 것이라 생각됨
\(\rightarrow\) N차원이 작아지면, 최대 \(\sqrt{N}\)만큼 분산의 영향이 커짐
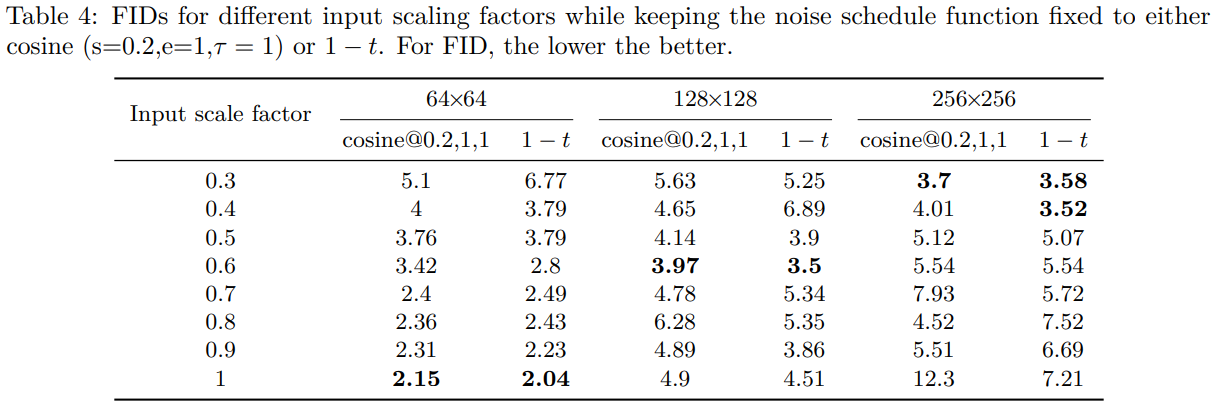
The effect of strategy 2 (input scaling)
Schedule function은 고정하고 input scale만 변경
- 이미지 크기가 커지면 optimal schedule의 input scale \(b\)가 작아지는 경향이 있음
- strategy 1보다 찾기 쉽고 성능도 좋음
- factor하나만 조절하면 됨
개인적인 생각:
- 이미지 사이즈가 작으면 노이즈의 영향을 많이 받음. 따라서, 평균 값을 조정하는 \(b\)가 더 커야함 (분산에 집중하기 위해)
- 이미지 사이즈가 크면, 인근 픽셀의 중복 때문에 shortwave의 영향이 작아지기 때문에 longwave인 평균에도 집중하는 것이 좋은 성능을 보임
- 혹은 b를 줄임으로써, 실질적으로 SNR이 주는 것이 noise의 영향을 크게한다고 해석할 수 있음
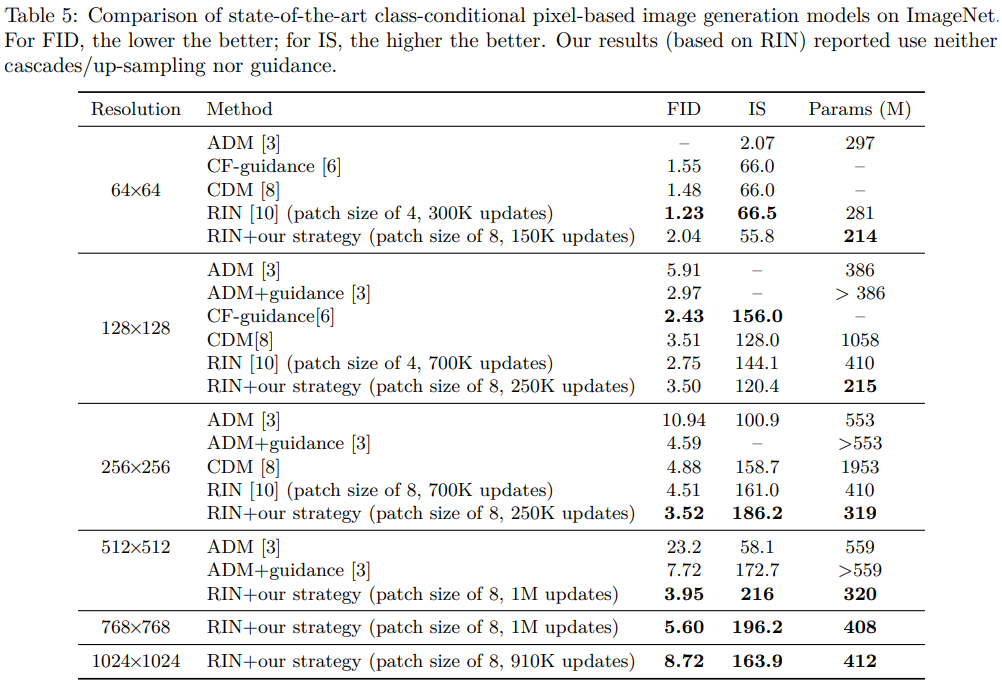
The simple compound strategy, combined with RIN, enables state-of-the-art single-stage high-resolution image generation based on pixels
RIN과 결합하여 고품질 이미지를 생성가능
저자는 Pixel-base DM에서만 테스트하고, latent DM은 테스트하지 않음
하지만 잠재적으로 latent에서도 동작할 수 있음