Denoising Diffusion Probabilistic Models
Denoising Diffusion Probabilistic Models
Table of contents
- TODO: 정리본 업데이트 (기본 수식 및 설명 정리)
- Introduction
- Background
- Diffusion models and denoising autoencoders
- Experiments
- Conclusion
- Appendix
TODO: 정리본 업데이트 (기본 수식 및 설명 정리)
Diffusion probabilistic models 과 denoising score matching with Langevin dynamics 사이의 연관성에 따라 설계된 Variational bound로 훈련됨
Autoregressive decoding의 일반화로 해석되는 progressive lossy decompression으로 볼 수 있음
Target distribution에서 noise를 추가하는 forward process와 noise에서 target distribution으로 복원하는 backward process의 distribution을 맞추는 것
Introduction
DM은 VI를 이용한 parameterized Markov chain
Signal을 파괴(Noise)시키는 Markov chain인 diffusion process의 reverse를 학습
\(\rightarrow\) Noise가 작으면 transition을 conditional gaussian으로 설정 가능 \(\mathcal{N}(x|\mu, \Sigma)\)
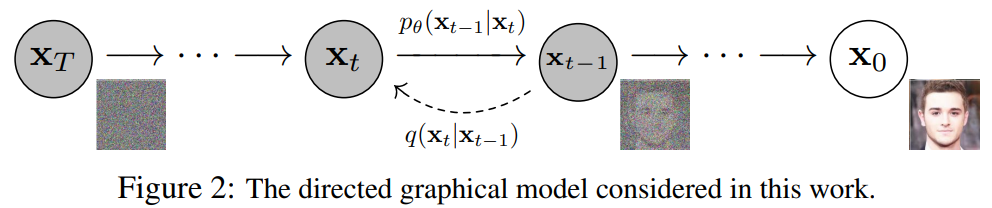
퀄리티는 좋지만, 다른 타입의 모델에 비해, NLL(lossless codelength)가 좋지 않음
이를 lossless codelength를 인지할 수 없는 이미지 세부 정보를 설명하는 데 사용
\(\rightarrow\) lossy compression으로 분석하여 AR과 비슷한 progressive decoding이라는 것을 보임
Background
DM은 latent variable models (Observable variable을 latent variable로 연결하는 statistic model)
\[p_\theta(x_0):= \int p_\theta(x_{0:T})dx_{1:T}, \quad \mathrm{where\;} x_1,\cdots, x_T \mathrm{\;are\;latent\;of\;data\;} x_0 \sim q(x_0)\]\(p_\theta(x_{0:T})\)는 reverse process로 불리고, \(p(x_T)=\mathcal{N}(x_T;0, I)\)부터 시작한 gaussian trasition의 MC
\[\begin{gather} p_\theta(x_0):= p(x_T)\sum^T_{t=1}p_\theta(x_{t-1}\mid x_t), \quad p_\theta(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t), \sum_\theta(x_t,t)) \end{gather}\]Probabilistic distribution을 구하기 위한 bayes’s rule의 posterior를 구하기 어렵기 때문에, 근사하기 위하여 사용되는 approximate가 noise를 추가해나가는 Markov chain에 고정되어 있음
\[\begin{gather} q(x_{1:T}\mid x_0):= \sum^T_{t=1}q_(x_t\mid x_{t-1}), \quad q(x_t\mid x_{t-1})=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_t I) \end{gather}\]훈련은 NLL에 대한 variational bound를 최적화하는 것으로 수행됨
\[\begin{gather} \mathbb{E}\left[-\log p_\theta(x_0)\right] \le \mathbb{E}\left[-\log\frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)}\right] = \mathbb{E}_q\left[-\log p(x_T)-\sum_{t\ge 1}\log\frac{p_\theta(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})}\right] =: L \end{gather}\]또한 \(\beta_t\)가 충분히 작을 때, forward와 backward는 같은 함수 형식을 가지기 때문에 표현력이 보장되고, \(\beta_t\)는 학습도 가능하고, hyperparam으로 설정할 수도 있음
임의의 t에 대해서 \(x_t\)는 closed form (\(x_0\)가 주어졌을 때)
\[\begin{gather} q(x_t\mid x_0) = \mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0, (1-\bar{\alpha}_t)I) \end{gather}\]따라서, 식 (3)에서 random한 t를 적용하여, 효과적으로 학습가능
식 (3)을 다시 적으면,
\[\begin{gather} L := \mathbb{E}_q\left[\underbrace{D_{KL}(q(x_T\mid x_0) \parallel p(x_T))}_{L_T} + \sum_{t>1}\underbrace{D_{KL}(q(x_{t-1}\mid x_t,x_0)\parallel p_\theta(x_{t-1}\mid x_t))}_{L_{t-1}}\underbrace{-\log p_\theta(x_0\mid x_1)}_{L_0} \right] \end{gather}\]Forward와 reverse를 KL divergence를 이용하여, posterior를 직접 비교
\[\begin{align} q(x_{t-1}\mid x_t,x_0) &= \mathcal{N}(x_{t-1};\tilde{\mu}_t(x_t\mid x_0),\tilde{\beta}_t I), \\ \text{where} \quad \tilde{\mu}_t(x_t,x_0) &:= \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0 + \frac{\sqrt{\alpha}_t(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} \quad \text{and} \quad \tilde{\beta}_t := \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t}\beta_t \end{align}\]두 변수 다 gaussian 형식으로 나오기 때문에 결과의 변동성이 큰 MC 대신 Rao-Blackwellized fashion를 사용할 수 있음 (?)
Diffusion models and denoising autoencoders
DM은 자유도가 높음
DM과 DSM 사이의 단순한 연결(섹션 3.2)과 DM을 위한 weighted variational bound objective (섹션 3.4)를 명시적을 설명
Forward process and \(L_T\)
\(\beta_t\)를 constant로 고정 \(\rightarrow\) 식 (5)에서 q는 학습가능한 변수가 X
\(\rightarrow\) \(L_T\)는 무시됨 (너무 작은 constant 값이기 때문)
Reverse process and \(L_{1:T-1}\)
Reverse process의 경우 다음과 같이 표현 가능
\[p_\theta(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t)), \quad \mathrm{for\;} 1<t \le T\]\(\Sigma_\theta(x_t,t)=\sigma^2_tI\)로 표현되는데, \(\sigma^2_tI\)가 \(\beta_t\)일 때와, \(\tilde{\beta_t}\)가 차이는 없음
\(\beta_t\)는 \(x_0\)가 가우시안을 따를 때, 최적이고,
\(\tilde{\beta_t}\)는 \(x_0\)가 한 점일 때, 최적
\(\mu_\theta(x_t,t)\)의 경우, \(p_\theta(x_{t-1}\mid x_t)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\sigma^2_tI)\)일 때, 아래로 표현 가능 (KLD 확인하기)
\[\begin{gather} L_{t-1} = \mathbb{E}_q\left[\frac{1}{2\sigma^2_t}\lVert\tilde{\mu}_t(x_t,x_0)-\mu_\theta(x_t,t)\rVert^2 \right] + C \end{gather}\]위의 식 (8)을 식 (4)와 식 (7)을 이용하여 확장 가능
식 4의 변형: \(x_t(x_0,\epsilon)=\sqrt{\bar{\alpha_t}}x_0 + \sqrt{1-\bar{\alpha_t}}\epsilon\)
\[\begin{gather} L_{t-1} -C &= \mathbb{E}_{x_0,\epsilon}\left[\frac{1}{2\sigma^2_t}\lVert\tilde{\mu}_t x_t(x_t,x_0)-\frac{1}{\sqrt{\bar{\alpha}_t}}(x_t(x_0,\epsilon)-\sqrt{1-\bar{\alpha}\epsilon})-\mu_\theta(x_t(x_0,\epsilon),t)\rVert^2 \right] \\ &= \mathbb{E}_{x_0,\epsilon}\left[\frac{1}{2\sigma^2_t}\lVert\frac{1}{\sqrt{\alpha_t}}(x_t(x_0,\epsilon)-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon)-\mu_\theta(x_t(x_0,\epsilon),t)\rVert^2 \right] \end{gather}\]즉, 식 (10)은 \(\mu_\theta\)가 주어진 \(x_t\)에 대해서 반드시 \(\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha_t}}}\epsilon)\)을 예측함
\(x_t\)는 \(x_0\)에서 직접 접근이 가능함
따라서 다음과 같이 표현 가능 (\(\epsilon_\theta\)는 \(x_t\)에서 예측된 입실론을 매개변수화 한 것)
식 11을 이용하여, 식 10을 다시 표현하면 아래와 같이, 입실론에 대한 매개변수로 표현이 가능함
\[\begin{gather} \mathbb{E}_{x_0,\epsilon}\left[\frac{\beta^2_t}{2\sigma^2_t\alpha_t(1-\bar{\alpha}_t)}\lVert \epsilon - \epsilon_\theta(\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t) \rVert^2 \right] \end{gather}\]즉, DSM을 닮은 objective function을 최적화하는 것은 Langevin dynamics와 닮은 샘플링 체인을 맞추기 위해 VI를 쓰는 것과 같음
요약하면, reverse process를 mean을 추정하게 훈련하거나, 재매개변수화로 noise를 추정할 수 있음
$\epsilon$-prediction은 Langevin dynamics와 DSM과 닮은 VI와 같음
Data scaling, reverse process decoder, and \(L_0\)
[0 ~ 255]의 이미지는 [-1 , 1]로 scaling되어, bounded된 영역에서 reverse가 수행할 수 있게 됨
하지만, continuous에 대한 image의 discretize가 필요하기 때문에 마지막 항을 gaussian에서 파생된 별개의 decoder로 설정
PixelCNN++에서는 이전 PixelCNN에서 sigmoid를 통해, class를 예측했었던 것과 달리, 인접한 픽셀값들의 inductive bias와 output의 randomness에 대한 discrete log likelihood를 구하기 위해 픽셀값의 분포를 예측함
이와 마찬가지로, DDPM에서도 discrete한 image 값에 대해 \(p_1\)분포를 바탕으로 log likelihood를 구함
\[\begin{gather} p_\theta(x_0\mid x_1)=\prod_{i=1}^D\int^{\delta_+(x^i_0)}_{\delta_-(x^i_0)}\mathcal{N}(x;\mu^i_\theta(x_1,1),\sigma^2_1)dx \\ \delta_+(x) = \begin{cases} \infty, & \mathrm{if}\;x=1 \\ x+\frac{1}{255}, & \mathrm{if}\;x < 1 \end{cases}, \qquad \delta_{-}(x) = \begin{cases} -\infty, & \mathrm{if}\;x=-1 \\ x-\frac{1}{255}, & \mathrm{if}\;x > 1 \end{cases} \end{gather}\]즉, \(x_1\)에서 \(x_0\)의 확률은, continuous를 discrete으로 만드는 것과 같다고 볼 수 있음
\(x_1\)의 분포에 대한 discrete의 확률이기 때문
따라서, \(\mu_\theta(x_1,1)\)는 노이즈가 없음
또한 이렇게 설정된 variational bound는 discrete data(이미지)의 lossless codelength를 보장함 (무손실 압축과 같은 말)
Codelength
NLL의 평균은 엔트로피와 같음. 여기서 엔트로피는 정보량이기 때문에 codelength로 표시하는 듯
bit per dimention은 정보량을 dimension에 따라 일관적으로 비교하기 위해 나눠주는 것PixelCNN은 픽셀 하나하나의 값을 계산함
즉, 1~255의 class에 대해서 cross-entropy loss를 계산
따라서, NLL은 픽셀값의 오차(손실)이라고 볼 수 있고, 이는 오차에 대한 정보량을 의미함 (GT와 얼마나 손실이 있었는지)
이 오차는 dimension의 크기에 따라 달라질 수 있기 때문에 resolution에 따라서 평균을 내주어, bit per dim으로 나타냄추가적인 내용
정보이론에서, 확률 분포에 음의 로그를 취한 것이 정보량이라고 할 수 있음 (\(I(x)=-\log P(x)\))
log의 밑이 2면 bit, 자연 상수 e면 nat의 정보량 단위를 가짐
섀넌 엔트로피 \(H(x)\)는 전체 data에 대한 불확실성을 나타내기 때문에, \(H(x)=\mathbb{E}_{x\sim P}\left[-\log P(x)\right]\)
\(\rightarrow\) 예를 들어, 동전 1개의 앞 뒤 \(H(x)=1\) bit, 2개는 \(H(x)=2\) bitCross-Entropy는 주어진 data에 대한 섀넌 엔트로피와 KL Divergence의 합이기 때문에,
CE loss는 두 분포의 KL Divergence를 minimize하는 것과 같음
즉, 밑을 2로하는 CE Loss의 값은 inference와 data의 분포 오차에 대한 정보량(bit)
Simplified training objective
식 (12)와 식 (13)에 의해, variational bound는 훈련할 수 있도록 미분가능해짐
하지만 다음과 같이 simplify하는 것이 더 좋음
\[\begin{gather} L_{simple}(\theta) := \mathbb{E}_{t,x_0,\epsilon}\left[\lVert\epsilon=\epsilon_\theta(\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t)\rVert^2\right] \end{gather}\]t = T일 때는 상수라 버려지고, t > 1일때는 식 (12)의 weight를 버림
식 (12)의 weight는 t가 클수록 더 큰 가중치를 매기는 것과 같음
\(\rightarrow\) t가 큰 것이 더 어려운 task라 집중하면 더 좋은 sample을 나오게 할 수 있음
\(L_0\)의 경우 gaussian으로 근사 시켜버림
Experiments
\[T = 1000, \beta_1 = 10^{-4}, \beta_T = 0.02, \mathrm{data scale}: [-1, 1]\]Architecture: Backbone of PixelCNN++,
Sample quality
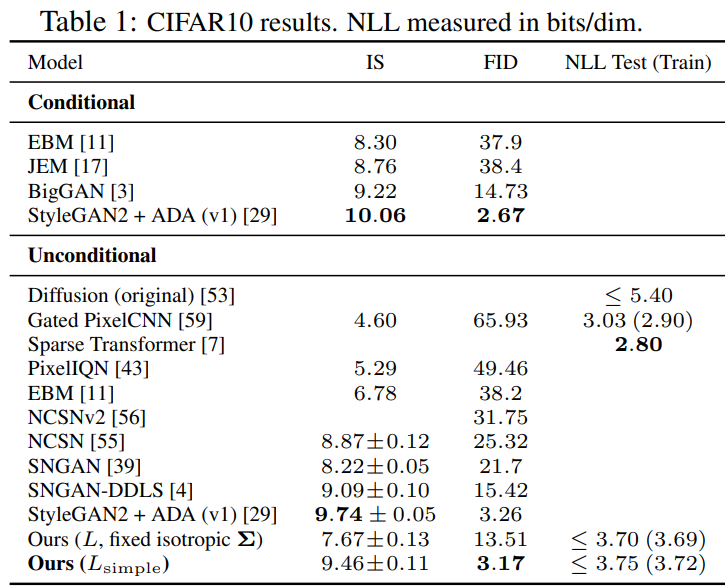
Reverse process parameterization and training objective ablation
epsilon의 경우가 L simple일 때 좋은 성능을 보임
mu는 variance를 훈련시키면, 불안정함
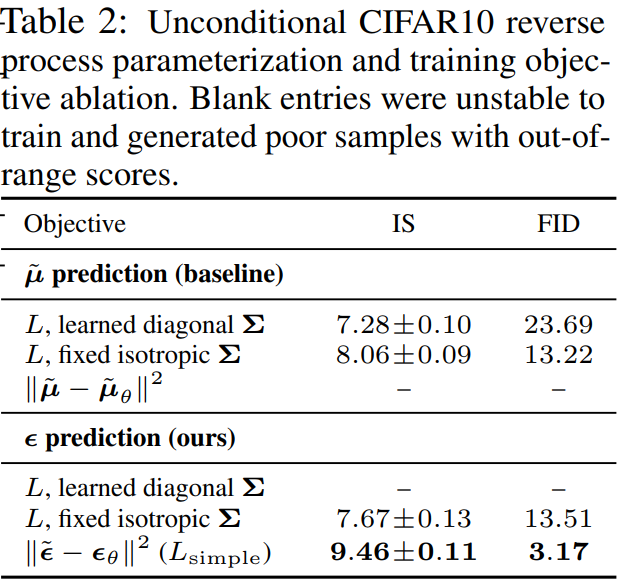
Progressive coding
NLL에서 train test가 0.03 차이나기 때문에 과적합은 피했음
하지만, NCSN보다는 성능이 좋음에도, 다른 생성모델보다는 경쟁력이 떨어짐
하지만 샘플의 품질이 높기 때문에 DM은 우수한 lossy compression을 만드는 inductive bias가 있다고 결론
Progressive lossy compression
Tab1에서 ours는 3.75의 NLL (lossless codelength)를 나타내는데, 이 중 rate(\(L_{t-1}\)) = 1.78, distortion(\(L_0\)) = 1.97 이지만, MSE는 0.95로, 절반 이상의 알수 없는 distortion이 생김 즉, pixel간의 차이말고 눈에 띄지 않는 왜곡이 발생했음을 알 수 있음
\[\begin{gather} L := \mathbb{E}_q\left[\underbrace{D_{KL}(q(x_T\mid x_0)\parallel p(x_T))}_{L_T} + \sum_{t>1}\underbrace{D_{KL}(q(x_t\mid x_t,x_0)\parallel p_\theta(x_t\mid x_t))}_{L_{t-1}}\underbrace{-\log p_\theta(x_0\mid x_1)}_{L_0}\right] \end{gather}\]위의 식을 이용하여 조금 더 분석
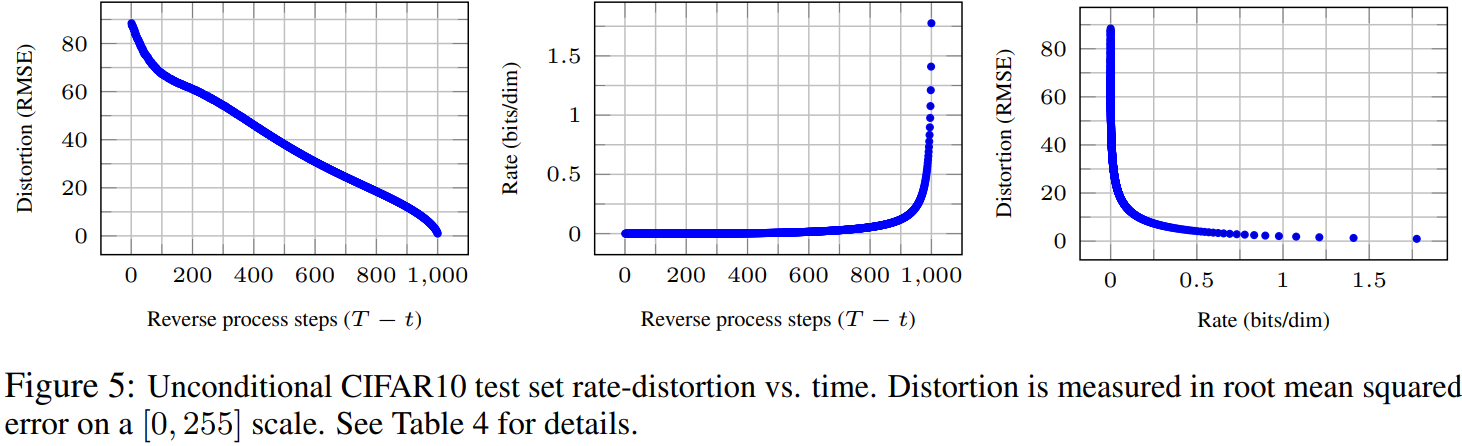
1~T의 각 step마다 \(x_T\)로부터 \(x_0\)를 복원해봄 (식 (4): \(\hat{x_0}=(x_t-\sqrt{1-\bar{\alpha_t}}\epsilon_\theta(x_t))/\sqrt{\bar{\alpha_t}}\)))

왼쪽 그림: 당연하게도 \(x_T\)에 가까울수록, 식 (4)로 \(x_0\)을 복원할 때, 왜곡이 큼
중앙 그림: \(L_{t-1}\)은 t가 0에 가까울수록 급격하게 커짐
오른 그림: distortion과 rate의 비율은 rate이 낮을 때, 즉 T에 가까울 때, 급격히 줆
\(\rightarrow\) 감지할 수 없는 왜곡이 있음
Progressive generation
이미지는 coarse부터 fine으로 생성됨
확률적 생성이기 때문에, t가 작을 때부터 공유될수록, 같은 이미지가 생성됨

t가 압축 비율로 비유되었을 때, 압축이 적을수록, 왜곡이 적다는 것으로 이해할 수 있음
Connection to autoregressive decoding
아래와 같이 Loss function을 다시 쓸 수 있음
\[\begin{gather} L = D_{KL}(q(x_T)\parallel p(x_T)) + \mathbb{E}_q\left[\sum_{t\ge 1}D_{KL}(q(x_{t-1}\mid x_t \parallel p_\theta(x_{t-1}\mid x_t)))\right] + H(x_0) \end{gather}\]이를 T 길이의 dimension data로 보고, \(q(x_t\mid x_0)\)는 처음부터 t coordinate까지의 가려진 것, \(q(x_t\mid x_{t-1})\)는 t번째 coord만 가려진 것이라고 가정.
이러한 상황에서 위의 식에서 첫항은 0이고, 중간항은 T부터 픽셀값을 하나하나 복사해나가도록 학습하는 것으로 취급할 수 있음
\(\rightarrow\) autoregressive의 한 종류로 취급
SPN에서는 scaling을 통해, 작은 이미지에 대해 먼저 AR을 수행하고, reordering 후, inductive bias를 바탕으로 더 수월하게 AR 예측
\(\rightarrow\) locality에 대한 inductive bias 수행
이렇게 subsampling에 대한 masking을 수행하여 Inductive bias를 주는 것보다 gaussian이 더 자연스럽고, reordering도 필요없음 (일반화됨)
따라서 inductive bias를 더 강하게 가지고 있을 것을 기대
또한 dimension에 국한되지 않음 (32x32x3도 1000 step으로 생성해냄)
Interpolation
두 source image \(x_1, x_2\)를 latent space (t 시점)으로 stochastic encoding하여 보간할 수 있음
사실상, pixel space에서 interpolation의 artifact를 제거하는 용도로 사용됨
그럴듯한 복원 성능, t가 클수록 다양한 보간을 만들어냄 (하지만, stochastic이라는 한계)
Conclusion
DM으로 고품질 샘플 생성
추가적으로, Diffusion model과 Markov chain 훈련을 위한 VI, DSM과 Annealed LD, autoregressive models, progressive lossy compression과의 연결을 발견, 제시
Appendix
A: AR 공식에 대한 유도 과정
B Experimental details
PixelCNN++의 UNet을 backbone으로 씀
C Discussion on related work
NCSN과 비슷하지만 다름
- Backbone architecture가 다름
- DDMP은 forward step에서 step마다, mean이 \(\sqrt{1-\beta_t}\)만큼 줄어들기 때문에 noise가 sampling 과정에서 추가되어도 variance가 유지(VP)되지만 NCSN(VE)은 아님
- Noise 추가 방식이 다르고, 이는 sampling 시 분포 이동을 방지
- Train과 동시에 samplar가 최적화되는데, NCSN은 train과 samplar의 hyperparam이 연동되지 않음
D Samples