S4
S4: Effciently Modeling Long Sequences with Structured State Spaces
Table of contents
S4의 저자들은 이전 논문(HiPPO)에서 LRD(Long-Range Dependency) 문제를 풀기 위해 Orthogonal Polynomial을 활용하여 시간에 따른 data의 함수 \(f(t)\)를 근사했다. Sequential Data의 online approximation을 위해 well-studied인 orthogoanl polynomial로부터 coefficient의 미분 \(\dot{c}(t)\)를 \(c(t)\)에 대한 식으로 유도한다.
\[\begin{align} \dot{c}(t)=Ac(t)+Bu(t) \end{align}\]이후, LSSL 논문에서 HiPPO framework를 SSM과 연결하기 위한 방법을 제시한다.
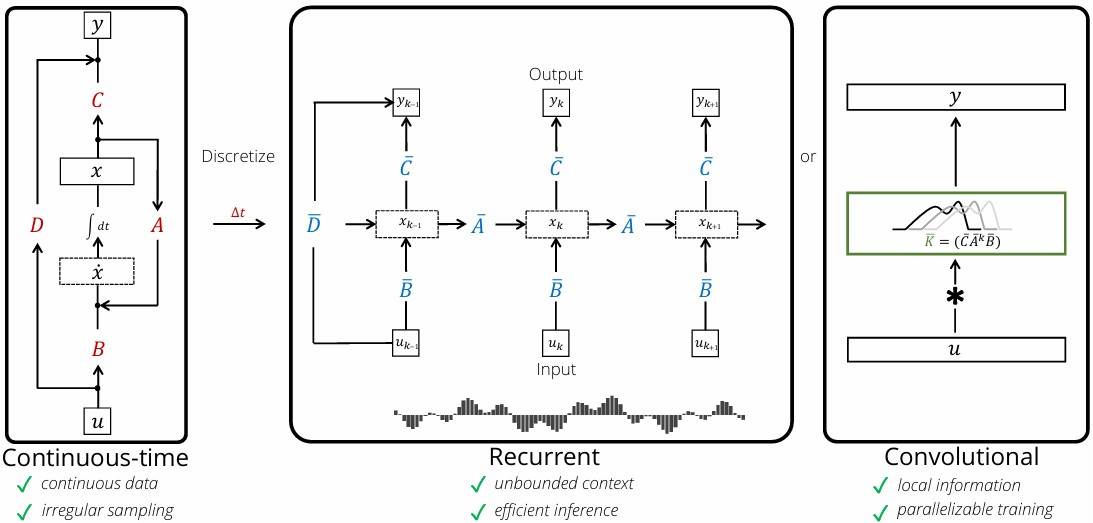
Linear State-Space Layer (LSSL)은 위 그림의 3가지 형태로 나타낼 수 있다. Continuous Time Data를 HiPPO framework의 A, B Matrix를 SSM과 결합하여 표현할 수 있고, discretize를 통해 discrete step-size \(\Delta t\)로 표현할 수 있다.
\[\begin{align} x(t+\Delta t)=(I-\alpha\Delta t \cdot A)^{-1}(I+(1-\alpha)\Delta t\cdot A)x(t)+\Delta t(I-\alpha\Delta t\cdot A)^{-1}B\cdot u(t) \end{align}\]SSM의 dimension \(n=1\)로 했을 때, Gated RNN과 동일한 수식을 가짐을 보이며 Reccurent한 성질을 보인다.
Convolutional form은 HiPPO의 discrete-time state-space model의 수식을 풀어서 얻을 수 있다.
의 수식은
\[\begin{align} x_0 = \bar{B}u_0 && x_1 = \bar{A}\bar{B}u_0 + \bar{B}u_1 && x_2 = \bar{A}^2\bar{B}u_0 + \bar{A}\bar{B}u_1 + \bar{B}u_2 \\ y_0 = \bar{C}\bar{B}u_0 && y_1 = \bar{C}\bar{A}\bar{B}u_0 + \bar{C}\bar{B}u_1 && y_2 = \bar{C}\bar{A}^2\bar{B}u_0 + \bar{C}\bar{A}\bar{B}u_1 + \bar{C}\bar{B}u_2 \\ \end{align}\] \[\begin{align} &y_k = \bar{C}\bar{A}^k\bar{B}u_0 + \bar{C}\bar{A}^{k-1}\bar{B}u_1 + \dots + \bar{C}\bar{A}\bar{B}u_{k-1} + \bar{C}\bar{B}u_k \\ &\rightarrow y = \bar{K} * u \\ &\bar{K} \in \mathbb{R}^L := \mathcal{K}_L(\bar{A}, \bar{B}, \bar{C}) = (\bar{C}\bar{B}, \bar{C}\bar{A}\bar{B}, \dots, \bar{C}\bar{A}^{L-1}\bar{B}) \end{align}\]로 정리되어 local information을 캡쳐하고 parallelizable training이 가능하다.
하지만, LSSL은 \(\bar{A}^{k}\)의 연산 문제로, 실질적인 구현 가능성이 낮다는 문제점이 있다. LSSL 논문에서도 efficient compute emthod를 제시하지만, S4 논문에서 계산 효율성을 더 집중하여 다룬다.
Method
Motivation: Diagonalization
S4의 목표는 식 (8)의 연산을 효율적으로 함으로써 compute efficient한 SSM Model을 설계하는 것이다. 따라서 \(\bar{A}^{k}\)을 효율적으로 연산하는 것을 목표로 하며, diagonal matrix는 거듭 제곱 연산이 쉽다는 것에서 S4 논문이 시작된다.
Diagonal matrix는 대각 성분만 제듭 제곱하면 되기 때문에 \(\bar{A}^{k}\)을 diagonal matrix로 만든다면 효율적으로 \(\bar{K}\)를 구할 수 있다.
\(x=V\tilde{x}\) ̃의 꼴로 x의 기저를 바꾸면,
\[\begin{align} \dot{x}=Ax+Bu && \rightarrow && \dot{\tilde{x}}=V^{-1}AV\tilde{x}+V^{-1}Bu \\ y=Cx && && y=CV\tilde{x} \end{align}\]와 같이 나타낼 수 있다. \(V^{−1}AV\)를 통해 바로 diagonal matrix로 바꿀 수 있으면 \(\bar{K}\) 연산이 매우 쉬워지겠지만 수치적으로 불가능함을 보인다. Matrix A를 diagonal matrix로 바꾸기 위한 V는 아래와 같은 이항계수 꼴로 나타난다.
\[\begin{align} V_{ij}=\binom{i+j}{i-j} \end{align}\]\(i,j\)가 커지면 V의 element값이 너무 커지기 때문에 computing에서 overflow가 발생할 수 있어, 현실적으로 연산이 힘들다. \(\rightarrow\) Appendix B.1 참조
따라서, 저자는 NPLR(Normal Plus Low-Rank)를 통해 연산 효율화를 수행한다.
The S4 Parameterization: Normal Plus Low-Rank
저자는 matrix A를 직접 diagonal matrix로 만들긴 힘들지만, normal matrix와 low rank matrix의 합으로 나타낼 수 있다는 것을 발견한다.
로 표현했을 때, \(V\Lambda V^*\)는 normal matrix, \(\Lambda\)는 diagonal matrix, \($P,Q\)는 각각 vector로 곱해져서 Low-Rank Matrix를 의미한다. \(V\Lambda V^*\)(fixed matrix)는 HiPPO framework의 system을 유지하는 역할, \($P,Q\)는 normal matrix로 근사된 HiPPO framework를 dataset에 맞게 finetune하는 학습 역할로 생각할 수 있다.
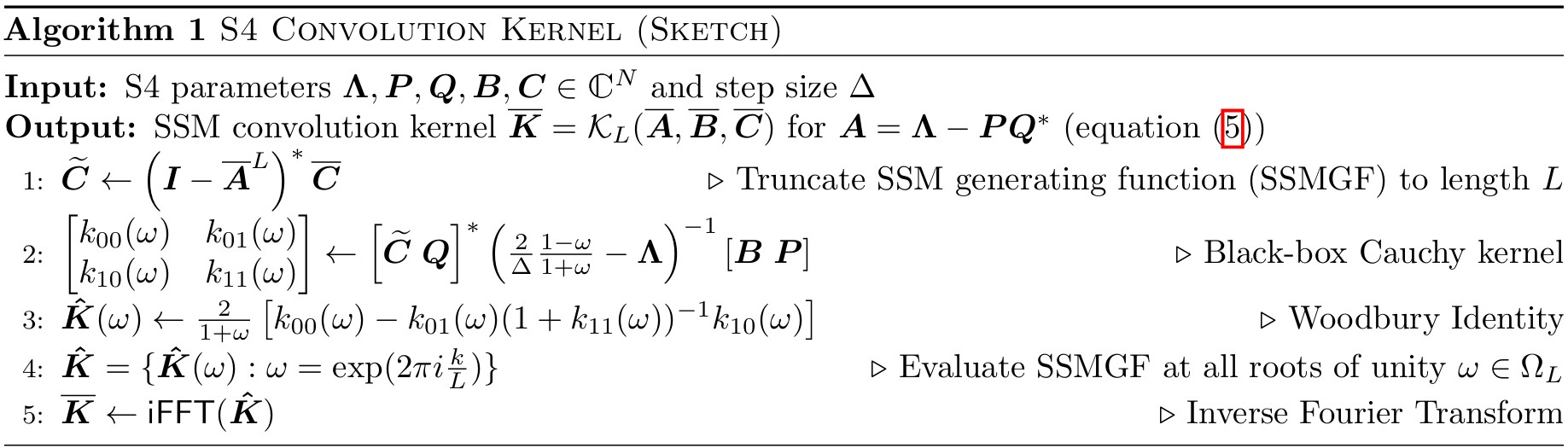
NPLR로 변환된 \(\bar{K}\)를 직접 계산하는 대신, GF(Truncated Generating Function)을 통해 역행렬 연산으로 바꿀 수 있다. 이는 z-transform 연산과 비슷한 흐름으로 생각할 수 있다.
Generating Function
\[\begin{align} G(z)&=I+zK+z^2K^2+z^3K^3+\cdots \\ &=I+zK+(zK)^2+(zK)^3+\cdots \end{align}\]
Kernel은 거듭 제곱 형식으로 나타나는 element의 집합이라고 볼 수 있다.
이런 elements (ex. \(K_1, K_2, etc\))를 계수로하는 임의의 z에 대한 다항함수를 생각해보면로 볼 수 있고 이를 형태 변환하면 (ex. 등비 급수 \(\frac{1}{1-r}\))
\[\begin{align}G(z)=(I-zK)^{-1}\end{align}\]의 꼴로 나타난다.
GF를 통해 변환된 역행렬 꼴 Kernel은 Normal Matrix + Low-Rank Matrix 이기 때문에 Woodbury Identity(전체 역행렬을 구하는 것이 아니라, normal matrix의 역행렬만 구하여 계산하는 방법)로 계산할 수 있다.
위의 전체적인 과정은 Cauchy Kernel을 푸는 것으로 귀결되며, z-transform과 비슷하게 convolution kernel을 주파수 영역에서 푼 것이므로 iFFT로 다시 \(\bar{K}\) ̅를 얻을 수 있다.
아래 표와 같이, 설계된 S4의 layer는 transformer에 비해서도 효율적으로 연산이 가능하다.

실제 Deep S4 Layer에서는 \(A\)가 right half-plane(복소평면에서 실수부가 양수(\(\mathcal{Re}(z)>0\)))일 때 불안정하다. 따라서 저자는 임의로 \(PP^T\)로 구현하여 잠재적 불안정성을 수정한다.
LTI System에서 고유값은 시스템의 동역학을 결정한다.
고유값이 right half-plane에 있다는 것은 시간이 지남에 따라 출력이 기하급수적으로 발산한다는 것을 의미한다.
이는 모델의 예측이나 변환이 수치적으로 불안정해져 의미 있는 결과를 얻기 어려워질 수 있다.